The Sierpinski triangle also called the Sierpinski sieve, is a fractal with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. This is one of the basic examples of self-similar sets–that is, it is a mathematically generated pattern that is reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but appeared as a decorative pattern many centuries before the work of Sierpiński.
Sorry, your browser does not support Canvas.
These triangles are drawn in much the same way many fractals are drawn. Using recursion.

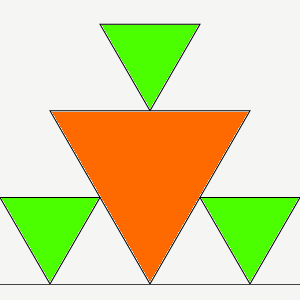We start with the triangle depicted in orange on the image to the left. The frame is updated so that we draw three triangles, half its size, adjoining it. A triangle placed on the left. This is done by shifting the x position left by half the size of the main triangle. A triangle placed on the right. This is done by shifting the x position point right by half the size of the main triangle. And a triangle on top. This is done shifting the y position by the length of the main triangle. The length of a triangle can be determined by the formula (size of triangle × (√3/2)). And finally we set each of the smaller triangles as the main triangle and recur from the beginning.

The source code is really easy to understand as well.
Show code