Simple Pendulum
22 Nov 2019
Here's a simulation of some simple pendulums. I think what surprised me most about coding this was the realization that the mass of the bob of the pendulum has NO say in its period. Only the length and the acceleration of gravity matter.

Sorry, your browser does not support Canvas.
VariableValue RangeValue
Gravity0.1 - 280 m/s

Presets :
Damping 0.900 - 1.000
Trace
FPS
Show/Hide


I know that the demo above looks very busy. You can turn off or on the pendulums and other animations on the demo and then you'll be left with just this realization. That behind all the "busy-ness" are just two calculations. One is to calculate the position of the bob of the pendulum based on the force and the other is to calculate the force itself.
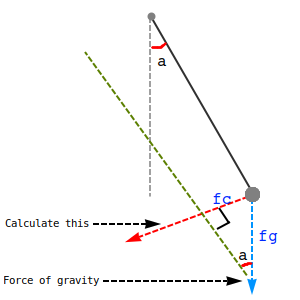On the image to the left, I did my best to explain the way to calculate the force on the bob of the pendulum. This is highlighted as the red line in the image (fc). We know the values of the following variables.
  1. The force of gravity (fg), highlighted by the blue line.
  2. The angle in radians (a) formed by the line parallel to the rod holding the rod. As a matter of fact it forms the same angle a the rod to the line perpendicular to gravity.
Now it is clear that this forms a right angled triangle. Thus we can use below formula to find the force. Note that I am using the SOHCAH method to get the formula.
SIN(a) = force to calculate (fc) / force of gravity (fg);
Thus fc = fg / SIN(a)
This gives us the force (or acceleration) that acts on the pendulum.
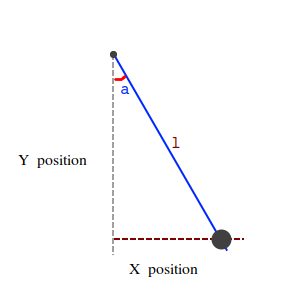Once we know the force, we know how fast or slow the angle changes. With the angle we can easily calculate the position of the bob. The image on the left shows how. We know two values. The angle (a) and the length (l). Using the SOHCAH method we calculate the position of the bob.
X Position = SIN(angle) * length
Y Position = COS(angle) * length
Finally, it is worth noting that the above demo assumes that the rod of the pendulum is mass-less. And that's it. That's how this is simulated.
1. pendulums.js - Download, index.html 
//Code goes here

Javascript Demos ▼

Here's a bunch of javascript... things I wrote over the years whenever time permitted.