Have you ever played Tic-Tac-Toe? I am pretty sure you have. Its a pretty simple game. It take all of 2 minutes to learn and just 10 minutes to master. You can play tic-tac-toe against the computer below.
State:
Player: 0
Computer: 0
Once you’ve mastered it, it’s a pretty easy game to win against a novice and easier to force a draw against an experienced opponent. You see, tic-tac-toe is a solved game. A solved game is a game whose outcome (win, lose or draw) can be correctly predicted from any position, assuming that both players play perfectly. There are many solved games. I was surprised to learn that Draughts (or checkers) is also a solved game.
So how would you play this game? I am sure it’s an iteration of thought process that goes something like this. “If I place my piece like so, then my opponent might place their piece like so, and to counter that I will place my piece like this” and so on and so forth. Essentially in your mind you are thinking of all the possible outcomes of placing a piece on the board. Strategy, I think the word we want to use here is strategy.
But you’ll realize that you have a limitation as to how many steps you can think ahead. How many moves can you think ahead? 3 moves, 4 moves? It is difficult to keep it in your head right? But not to a computer it’s not.
This is where the “minimax” algorithm comes into play. The minimax algorithm is used in many games including Chess and Draughts. It’s easiest to implement it for tic-tac-toe. Essentially it's a way to predict every move that is possible given the state of the board and score the moves based on its final outcome. The best winning score is chosen to play the current move. And this is only possible because we have powerful computers which can predict so deep.
But how deep? How many steps ahead is reasonable? This question is important because if a 3 x 3 tic-tac-toe playing computer plays first and if it needs to calculate all possible opening moves, then it needs to calculate 9! (9 factorial) moves or 3,62,880 moves. This is of course not an accurate calculation because we will have to eliminate those moves that result in wins or losses or draws (that's where the game ends) from our calculations. Yet, this number is close to being accurate because the first move needs to be played by placing a piece on every location on the board. Thus I can safely assume that the number of moves is a huge number. This is fine for a 3 x 3 tic-tac-toe game. In fact the computer won't even break a sweat calculating this. But what about a 4 x 4 board? What about Draughts or Chess? That's why it's important to remember that any implementation of the minimax algorithm must consider the depth of calculations. In other words, how many moves ahead should I predict so this an be played on a reasonably modern computer?
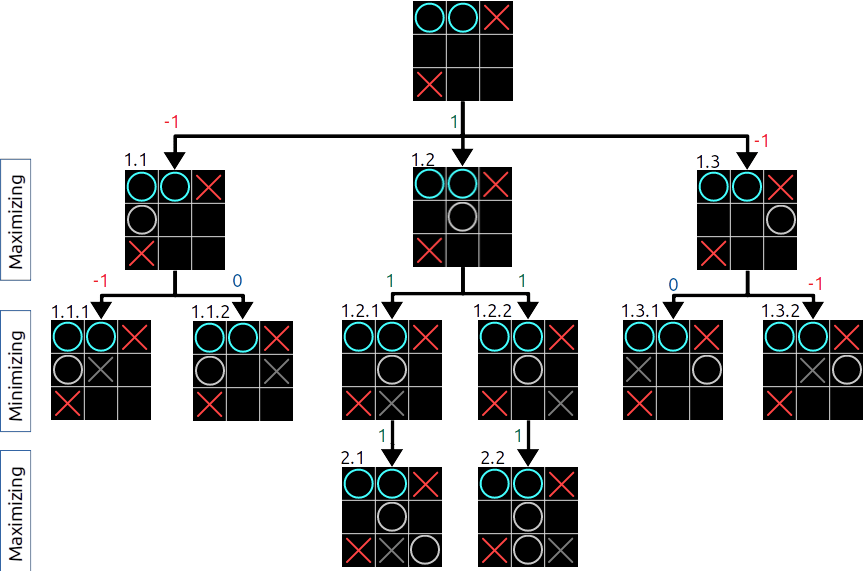
"Minimax" is short-form of "Minimizing"/"Maximizing". When the computer starts predicting (playing all moves) it needs to place alternating places on the board. One for itself and one for the human. It's own move is called "Maximizing" and the human move is called "Minimizing". In this prediction cycle it's necessary to keep score. if the computer predicts its own win then the score is increased, otherwise the score is reduced. Here's a board state with just 3 moves remaining. The next move is going to be the computers' move. Let's calculate the possible outcomes of this game and calculate the score using the Minimax algorithm. Look at the below image. I am hoping that this is a good approximation of what is happening with the minimax algorithm.
Before I begin explanation, lets draw a table with labels that shows indices of the game board so are all on the same page.
| 0,0 | 0,1 | 0,2 |
| 1,0 | 1,1 | 1,2 |
| 2,0 | 2,1 | 2,2 |
Now that this is established. Lets assume that the board starts with a state where the human has just put their piece (X) at position 0,2. The computer then calculates the next best move by placing its piece (O) in every place available place on the board.
- If the computer makes a move as depicted by board 1.1, the very next move (1.1.1) is a Minimizing move that clearly shows the human winning. That's why this whole tree (1.1) has a score of -1.
- If the computer makes a move as depicted by board 1.2, the Minimizing calculation shows that this has put the human in a dilema. No matter what they do, the computer will win the board. Thus, this tree is given a score of 1.
- If the computer makes a move as depicted by board 1.3, the next move (1.3.2) is a Minimizing move that clearly shows the human winning. That's why this whole tree (1.1) has a score of -1.
Thus the best move for the computer to play is move 1.2. This is ultimately what is chosen. The image above, obviously, does not show all the possible moves. This is because I would have run out of space drawing everything. But rest assured, the computer does calculate every move. Do have a look at the code below. I have appropriately commented it. You will also notice that it is probably impossible to defeat the computer. You can play around with the variable "targetDepth". A lower value of this variable may allow you to win.
Javascript Demos ▼
Here's a bunch of javascript... things I wrote over the years whenever time permitted.